
地產公司做項目測算時大多會著重看兩個指標,凈利潤率和irr。
凈利潤率為靜態指標(不考慮資金的時間價值),irr為動態指標(考慮資金的時間價值)。
相對來說irr較為復雜。
這篇文章主要跟大家分享下我對irr的理解。
我是地產運營崗的,會經常接觸到這些指標,當然也聽到過一些同行的觀點。
他們覺得運營不是財務,沒必要深入了解這些數字,在他們看來這些都是數字游戲,運營還是要下沉到項目。
雖然我知道大多數地產從業者不需要懂這些數字一樣能把工作干的出色,但是我仍然對這個觀點持反對意見。
我認為遇到不懂的就去探索才是該有的工作態度、生活態度。所以這篇文章只為想要了解和探討的人而寫。
01
irr怎么算
看到這個標題,許多同行哈哈大笑,肯定想這有什么好講的,用excel里求irr的公式=irr()一拉不就出來了,村口燙頭的王師傅學五分鐘都能算出來。
但是王師傅只知道irr用excel怎么求,卻不了解求irr背后的邏輯,我相信有相當一部分同行也是如此。
所以我需要講一下irr的計算邏輯,因為如果你想真正了解一個東西,就必須得知道它到底是怎么來的。
舉個例子:
象牙山的包工頭亮仔聽說養豬能賺錢,準備搞個養豬場。村里有個土豪叫阿強,有幾百萬存在余額寶,于是他便去說服阿強一起投資。
他跟阿強商量好,阿強第一、第二年每年投資100萬,第三年分阿強200萬,第四第五年分別再分阿強50萬。
為了說服阿強,亮仔給阿強引入了一個概念叫內部收益率,同時寫出了下面的現金流表:
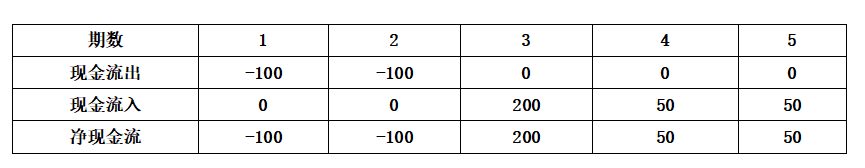
阿強問亮仔:內部收益率是啥?
亮仔解釋:【資金流入折現值總額與資金流出折現值總額相等、凈現值等于零時的折現率。】
阿強:講人話。
亮仔:通俗的意思就是設折現率為x,把凈現金流每一期的數字用折現率x一一折現到第一期,令所有數字相加等于0,這時候折現率x就是內部收益率。(注:關于折現率的基礎概念不再解釋,可以查閱資料)
接著亮仔在紙上列了一個方程式:
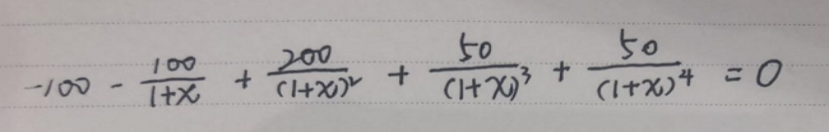
最終亮仔將方程式整理成了一個一元四次方程式,這個方程式的解x就是凈現值為0的收益率,也就是內部收益率。
以上就是利用irr的概念用數學方法列出的一元多次方程式,通過感受這一過程能夠讓大家更好的理解irr是怎么求出的。
但是解這個方程式很難,所以一般我們還是會運用excel快速求出irr。
這里有思維活躍的同學已經想到一件事,那就是一元四次方程式理論上有4個解,關于多解的問題后面會詳細說到,這里先不深入講。
02
irr到底是什么樣的收益率
接上面的故事:
亮仔告訴阿強,手算出內部收益率太難,于是打開電腦用excel中的irr函數求出了內部收益率是22.9%。

亮仔略帶一絲不易察覺的狡黠微笑告訴阿強:你看你這次投資我的養豬項目的年化收益率是22.9%,難道不比你放在余額寶里面香?
阿強心想22.9%的年化收益率還真的挺高的,以自己目前的資源根本找不到這么高收益率的投資機會。但是愛鉆牛角尖的大熊還是決定驗證一下:
第一年投資的100萬,到第五年項目結束后,獲得的收益是100*(1+22.9%)^4=228萬;
第二年投資的100萬,到第五年項目結束后,獲得的收益是100*(1+22.9%)^3=186萬;
二者相加355.5+258.9等于414萬。
阿強算完大吃一驚,前兩年投了200萬,到最后竟然能拿到414萬?可是從跟亮仔商量的方案上來看自己也只拿到了300萬呀,這剩下的114萬哪去鳥?
一旁的亮仔沒想到平時看起來傻傻的阿強會真的認真算一遍,尷尬的站在一旁冒冷汗。
阿強認為亮仔在騙他,瞬間怒火中燒,使出一招猴子偷桃,右手成爪直取亮仔要害。亮仔見狀左腳踩右腳騰空而起,跳上了旁邊的墻頭。
兩人一高一矮隔空對峙。
就在兩人大喊絕招準備正面硬鋼之際,正在一旁掃地的老頭大熊腳踏七星連行七步以一種不可思議的速度出現在兩人中間,隨即一招太極云手化解了兩方的攻勢,制止了雙方的進一步動作。
大熊詢問了沖突起因后,對兩人道:
“你們碰見我算是遇到對的人了,我年輕時候的本科專業是工程管理,學習過工程經濟學,里面就有講到這個內部收益率,我對此略知一二,就讓老夫幫你們評斷一下。”
大熊思索片刻,接著說道:
其實亮仔算的內部收益率沒有問題,但是如果簡單的將內部收益率理解為年化收益率就有點問題。阿強你想知道為什么少了114萬對嗎?
原因是我們求解內部收益率的前提是默認了【資金具有時間價值】。
所以如果你把第三年拿到的200萬和第四年拿到的50萬以22.9%為收益率再投資出去,加上第五年當年收入的50萬,就等于你的414萬。
阿強聽完開始動筆驗證:
第三年的200萬以22.9%的收益率再投資出去,到第五年獲得的收益是200*(1+22.9%)^2=302萬;
第四年的50萬以22.9%的收益率再投資出去,到第五年獲得的收益是50*(1+22.9%)=62萬;
加上第五年的50萬收益,三者相加302+62+50=414萬。
這時一旁的亮仔附和道:“你看,這414萬不就有了嘛……”
阿強的怒氣再次被點燃;“有個錘子,我要是能隨隨便便找個一年22.9%的收益率的投資機會我能把錢存余額寶?我看你是成心耍我!”
說完欲再次動手。亮仔趕緊向大熊投去求助的目光,大熊無動于衷。
亮仔偷偷向大熊伸出一根手指頭,大熊搖了搖頭,亮仔伸出了三根手指頭,大熊欲轉身要走,亮仔無奈,張開五根手指對著大熊。
大熊見到后,趕忙上前再次攔住阿強,說:“且慢動手,聽我細細道來,這個收益率22.9%也不是不無道理……”
(作者注:這里其實講到了irr的一個隱含假設【收益再投資】,大家若是把irr理解成年化收益率,把每期投入按年化收益率22.9%折到項目結束,就存在隱含假設【收益再投資】,這時候求出來的irr越高,此種理解方式越不合理。因為沒有辦法隨隨便便就找個這么高回報的投資機會……)
大熊頓了頓,眼珠子一轉:
阿強你仔細想想,其實你到了第三年之后便開始陸續回收你的資金,所以你用100*(1+22.9%)^4+100*(1+22.9%)^3=414其實也存在某些層面的不合理。
你換一種思路,你依然將22.9%看成年化收益率,只是這個年化收益率是你投進亮仔這個項目中未回收的本金及利息的收益率,這樣你再看看有沒有道理。”
于是按照大熊的說法,阿強重新列了一個表格:

果然,這樣一算,到最后一年剛剛好回收完所有待回收的本金及利息。
阿強思考片刻覺得這樣的確說得通,總的來講確實也比自己放在余額寶收益多,于是跟亮仔達成協議便回家去了。
大熊默默的收下了亮仔的五百塊美滋滋的走了。亮仔一個人在風中凌亂,感嘆知識就是金錢。
上面這個故事中包含了兩種理解內部收益率的角度,在此進行一個總結:
第一種角度:
將內部收益率當成年化收益率,在項目中的投入都按這個收益率來進行復利計算,一直到項目結束,這樣會得到一個理論上的收益。
但是這里會有一個隱含假設【收益再投資】。
只有將項目期間得到的收益同樣以內部收益率進行再投資,最終得到的收益才會等于你前期的投資在復利計算下最終得到的理論收益。
這種理解角度的缺陷在于內部收益率越高,【收益再投資】的假設越不合理。
第二種角度:
仍然將內部收益率看成年化收益率,但是僅僅是尚未回收的本金利息和的年化收益率。
因為項目后續是不斷開始返還收益的,所以實際上在這個項目中投入的資金并不是一直這么多的,是存在一個【投資回收的過程】的。
項目在全周期內始終處于一個投資回收的過程中,就避開了【收益再投資】這種蛋疼的假設。
所以一個投資項目的內部收益率要想合理,那么這個項目必須在整個周期中始終處于一個投資回收的過程。
以上所有的內容都基于投資的項目是常規項目,現金流規整。
若遇到非常規的項目,現金流不規整,可能無法使一個項目始終處于一個投資回收的過程,那這樣的內部收益率將不具有合理的經濟含義。
03
關于irr多解
上面已經講過怎么列求解irr的方程式。
下圖中,將原方程式整理一下,再令1+x=y,這樣整理出的方程式其實本質上就是一元n次方程式,而一元n次方程式的根有n個。

當我們需要用irr這個指標時,我們的前提條件是irr只有惟一正根。若irr存在多個正根,則這個項目已經不適用于用irr來進行判斷。
那么我們就需要利用一套數學理論來判斷irr究竟存不存在多個正根,這里拋出一個知識點叫笛卡爾符號律:
笛卡兒符號律是估計實系數多項式正根個數的一種方法,它斷定實系數多項式f(x)=a0x^n+a1x^n-1+…+an正根個數等于f(x)的系數列a0,a1,…,an的變號數減去一個非負偶數(0是偶數)。
設:f(x)=a0x^n+a1x^n-1+…+an,
其實系數序列a0,a1,a2,a3......an有μ個變號,而f(x)=0有p個正根,則
(1)p≤μ;
(2)p=μ-偶數
將上面的文字用人話解釋一下就是irr的正實數根的個數不超過項目的凈現金流由負到正或由正到負的次數。
舉例:x^3+x^2-x-1=0
這是一個一元三次方方程式,應有三個根。這個公式第二項到第三項由正到負,變化了一次,這個項目只有一個正根。
用一元三次方程式求解器進行驗證,該方程式的根為1和-1(二重根算兩個根),共3個,其中一個為正實數根,與推論一致。

舉例:x^4-x^3+x^2-x-1=0
這是一個一元四次方程式,應有四個根。符號變化了三次,則這個方程可能有3個正實數根或者1個正實數根。
用一元四次方程式計算器驗證,該方程一個正實數根,一個負實數根,兩個復數根,共四個根,與推論一致。
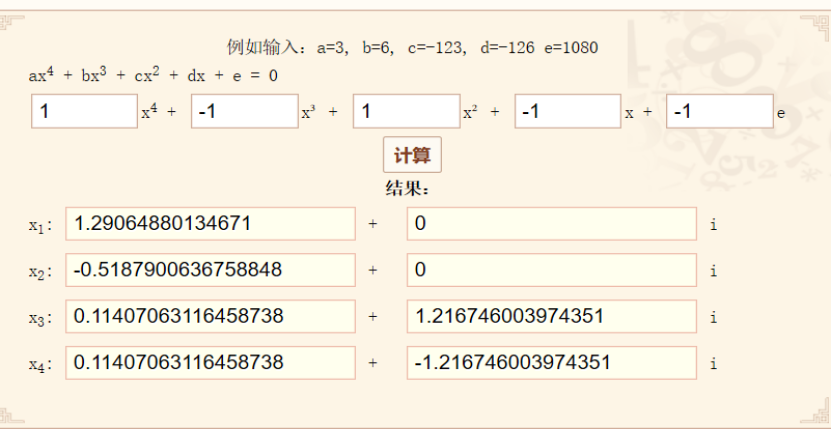
運用到實際求irr的操作中,可以總結出來這樣幾條規律:
1、當凈現金流的符號沒有出現變動時,全負或者全正,那么該方程的y(也就是1+x)無正實數根,那么同樣irr(x=y-1)無解。
2、當凈現金流的符號變動一次時,如開局一期或者若干期凈現金流為負,后續持續為正(一般的項目都是前期投入,后續開始回收資金),這時候irr有三種可能,0、正實數、負實數。
分析如下:
因為符號變動一次,該方程的y有一個正實數根,但是這里要注意,并不是說irr(x=y-1)就一定是正實數。因為我們知道當y為正實數時,x存在3種情況:
若1+x=1,則x等于0;
若1+x大于1,則x大于0,這里irr為irr為正實數;
若1+x大于0且小于1,則x小于0且大于-1,這里irr為負實數。
這里再對應上面三種情況舉三個具體的例子幫助大家理解:
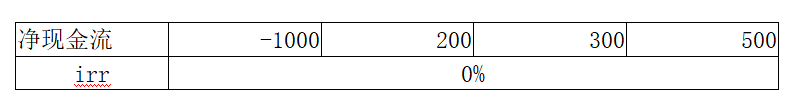
(1)符號變動一次,且累計現金流等于0的時候,irr為0。
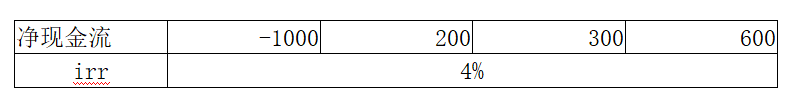
(2)符號變動一次,且累計現金流大于0的時候,irr有唯一正實數根。
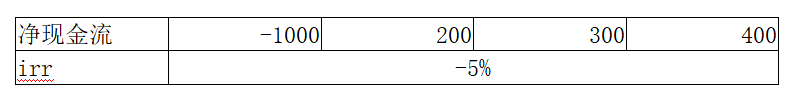
(3)符號變動一次,且累計現金流小于0的時候,irr無正實數根,且至少有一個負實數根。
這里有個細節,我并沒有寫唯一負實數根,因為當符號變動一次,累計現金流小于0時,求出來的負實數根irr并不一定只有一個,但是負實數根沒有討論意義,所以不再深究。
所以當符號變動一次的時候,只有當累計現金流大于等于0的時候,求出來的irr才是有意義的。
3、當現金流的符號變動多次時,如前期為負,后面為正,然后又為負......像這種符號反復變化的,那么該方程的y(也就是1+x)可能有多個正實數根,也可能有唯一的正實數根,也可能沒有正實數根。那么同樣irr(x=y-1)就沒辦法確定。
其實符號變動多次才是我們在做項目測算時的凈現金流的常態,因為幾乎沒有項目的凈現金流是很規整的按照我們想要的那樣前期為負后續為正只變動一次符號的。
因為大多數項目清盤后,項目還是在建狀態,后續的凈現金流就完全屬于流出狀態。
也就是說一個項目至少都會經歷這種負-正-負這樣的凈現金流模式。
更別說銷售期間沒有持續供貨導致中間一段時期沒有銷售回款或者當期支出多于當期銷售回款導致當期凈現金流為負這種情況。
也就是說根據實際情況來看,房地產項目的凈現金流至少也會變動兩次符號,甚至變動更多次導致irr可能存在多解。
(理論上也存在只變動一次的情況,就是這個項目隨著項目的建設一直銷售到項目完工,且保證每一期的回款都大于當期的支出,個人覺得這種情況不太多見)
也許有同行會說,我做測算雖然凈現金流符號變動多,但是用excel算的時候基本每次都給我返回一個正實數,感覺沒啥問題呀。
這里再給大家講一個知識點,用excel求irr的時候,無論有多少個irr的解,excel永遠只會返回其中的一個。
因為excel計算irr 的規則是默認這個數字在0.1附近,然后一個一個數去試算,直到有一個解使凈現值等于0,就會返回那個解,但是不會繼續去尋求第二個解。
所以這就是irr無論有多少個,而excel只會返回一個。
這時候可以用公式=irr(數組,guess)進行求解,guess是人為給定的估計值,通過調整guess的值找到其他解。
其實這種方法也只是理論上可行,實操基本沒法辦到,在不知道多少個解,不知道解是多少的情況沒辦法準確給定估計值。
這里舉幾個例子加深一下大家的感受:
例1(累計現金流等于0的情況):

這筆凈現金流符號變了四次,根據之前的理論y有4,2,0三種正實數根的可能,那么irr最多有4個解。
用求irr公式返回的結果是0。那么是否還存在其他的解呢,這時候我們利用一元四次方程式求解器看一下:
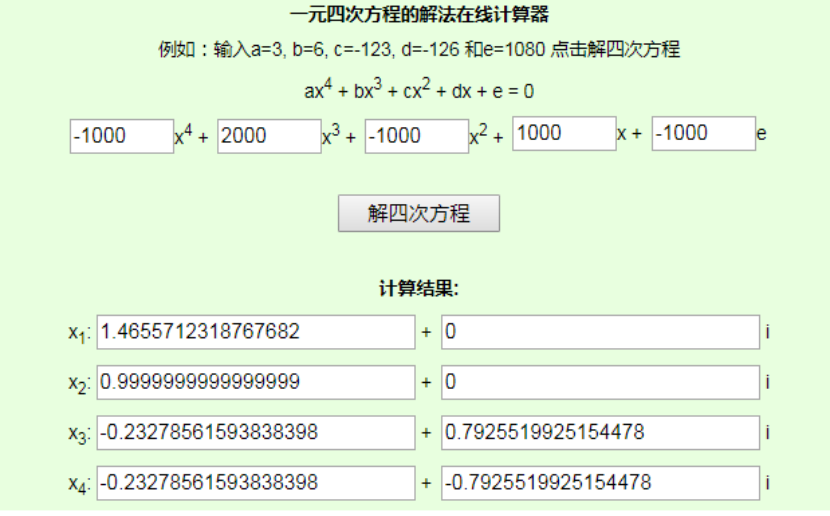
其中X2=0.9循環就是excel返還的irr的其中一個解0(0.99循環-1=0),那么X1就是另外一個解。另外一個irr是1.47-1=0.47。
代入excel驗證:

添加一個guess值0.47,irr果然返回了47%。
這里想問大家,當累計現金流等于0時,irr等于0和47%究竟有什么經濟含義?
0%還勉強說得通,這個47%代表啥,當然你要讓我強行解釋我也能解釋,可以跟上面講的irr的含義聯系起來看。
第二期的2000與第四期的1000以47%的再投資收益率投出去然后折到第五期,這樣算到最后應該等于第一期,第三期以及第五期的投入按47%的收益率折到第五期的和。
當然這也是理論上的解釋,并沒有什么實際的經濟意義。因為47%收益率的投資項目不好找。
頂多就是說這個投資項目對急需現金流的人或者公司有好處,雖然最后賬面上的數字是0。
但是我第一年投資1000萬,第二年就收到了2000萬,對于現金流比較緊張的公司來講,這是一個有益的地方。
例2(累計現金流小于0的情況):

這筆凈現金流符號變了四次,根據之前的理論y有4,2,0三種正實數根的可能,那么irr最多有4個解。
同時我們發現累計現金流小于0,意思就是利潤額為負,利潤率就是負的。再一看,irr求出的解竟然是12%。
通過一元四次方程式在線求解器看看方程解的情況:
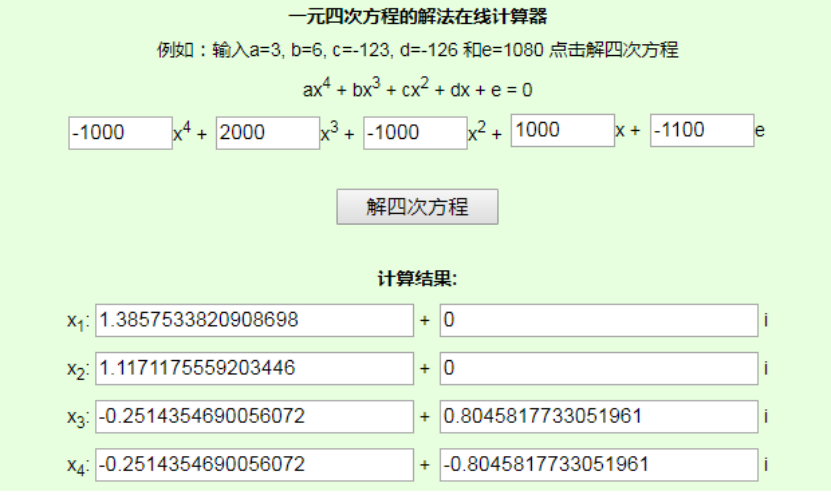
X2是1.12也就是我們已求出的12%(x=1.12-1),X1是1.39,那么另外一個irr就是1.39-1=0.39。
用excel驗證:

這樣求出兩個irr分別為12%,39%。這兩個irr同樣的對于一個累計現金流為負的項目沒有任何實際意義,惟一牽強的解釋仍然是我上面講的再投資的情況。
同時對于現金流緊張的企業相對來講有益。
例3(累計現金流大于0的情況):

其實大多數地產的項目凈現金流都類似于這樣,符號變動多次,因為最終有利潤,所以累計現金流大于0。
這個項目凈現金流變化了四次,根據之前的理論y有4,2,0三種正實數根的可能,那么irr最多有4個解。
直接跟上面用一樣的方法求出irr最終為兩個,71.7%和-76.8%。
這時候有人會說,irr存在唯一正實數解71.7%,那這個irr是不是也是合理的呢。我們直接以第二部分講過的兩個角度來分析。
第一種【收益再投資】的角度:
第一期,第三期跟第五期的投入分別以irr為收益率折到第五期:
1000*(1+71.7%)^4+1000*(1+71.7%)^2+200=11839
第二期、第四期的收益再投資:
2000*(1+71.7%)^3+1000(1+71.7%)=11839
理論上解釋的通,實際沒有經濟意義,因為你辦法將你在項目上獲得的收益以這么高的收益率再投資。
第二種【投資回收】的角度:

我們發現本來看起來說得通的投資回收看irr的角度也出現問題了,因為第二期的時候發現不僅投資連本帶息全部回收,還多了2000-1717.28=282.72。
這時候只能走上收益再投資的老路,將多出的錢以irr為收益率再投出去,到最后一期才能剛剛平掉。所以這里的唯一irr也變得沒有實際的經濟意義。
所以當凈現金流符號變動多次時,excel上給你返回的irr不再有任何意義。
到這里我們總結發現,一旦扯上【收益再投資】,所有東西都變得沒有意義。那么我們只有避開它,irr才有意義。所以我們得出結論:
在整個投資項目的周期內,始終保持住投資回收的狀態,每一期都有還沒回收的投資,這樣才不會涉及再投資收益的假設,這樣irr才有真實的經濟意義。
在大多數地產公司的測算表中,irr只是簡單的用=irr()對一個符號變動多次的凈現金流進行求解,excel返回的值就被默認為irr,不管這個數字有多大。
我曾經指著一個100%多的irr問一個同行,為什么irr會這么大,他似乎也沒有說上來。
只是說高周轉項目一向求出來的irr就是這么多,而且很多公司都是這么求的,應該沒啥問題。
一向如此,便對嗎?
正是帶著這個疑問,我才對irr起了興趣,才有了今天這篇跟大家交流探討的文章。
當然,我也看到過有些投模表比較心細的在求irr的這個環節做了一些小設計。
比如我現在所在的公司在求irr時候,先將凈現金流里當期為負數的凈現金流通過事先設定好的一個折現率統一折現至第一期。
這樣就形成了第一期為負,后續現金流均為正的這種狀態,通過將現金流提前規整,使求解過程符合邏輯。
雖然這樣操作求出來的不能算是嚴格意義上的內部收益率,但是至少相對合理,同時說明設置表格的這個人是有心的。
這里同時也拋出一個問題給各路同行,是否在這個指標求解的合理性上有其他好的辦法。
文章到此就結束了,歡迎同行交流指正。