
在投資圈似乎有一個奇妙的現象,投拓人們不管理不理解什么是IRR,反正都像“智能AI”一樣“熟練地”操練著Excel模型。
但在操作過程中,經常會出現一系列的問題,比如:
現象1:平時操作的IRR均能輸出正常的數,但這次突然顯示#NUM!;
現象2:項目的銷售凈利潤明明為正,可計算出來的IRR卻為負數;
現象3:項目的現金流目測很差,在銷售周期內基本沒辦法回正,可計算出來的IRR卻為正數。
……
因此,IRR逐漸變成了一個魔幻的概念,永遠算不準的玄學,更有人戲稱IRR和量子力學物理量一樣,測不準才是正常的(海森堡測不準原理)。
很多人筆者說很多軟文都在講IRR,看完好像明白了,似乎睡一覺又忘記了。
筆者這次選取的角度嘗試從IRR的生活視角出發,根據不同場合的變式衍生IRR的兄弟指標XIRR和MIRR,也許看完一次也是各位也會似懂非懂,那就請大家再多看一遍嘍~
概念篇:IRR與銷售凈利率的區別
各個公司在拿地時的投資指標可能會根據不同的關注點有所調整,部分公司也是根據不同的運營策略將投資指標分為“現金流型”、“均衡型”與“利潤型”;
但無論怎么變換調整,最基礎的指標仍然是銷售凈利率這一指標。
【例1】某項目經過各部門可研測算后,得到測算數據如下:
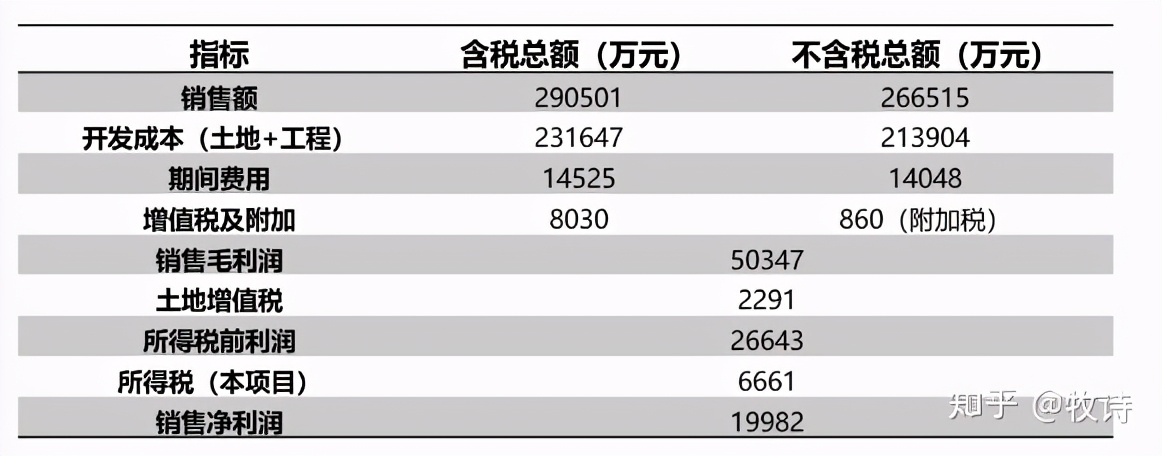
銷售凈利率是一個比值,從收入的角度看利潤。本質含義為可售單方利潤,與可售單方成本,可售單方費用。
可售單方稅費等是一個起跑線上的指標,也就是在每銷售出一元錢的收入,需要付出的成本多少?需要付出的費用是多少?需要付出的稅費是多少?最終留下的利潤是多少?
銷售凈利率的引申含義為:企業在增加銷售收入的同時,必須相應的獲得更多的凈利潤,才能保持銷售凈利率穩步不變或有所提高。
因此:
IRR為什么叫內部收益率?
1、本質與銷售凈利率的衡量視角不同,銷售凈利率是單一的資金視角。
誠如上文所說,銷售一元錢,最終折成利潤是多少錢,但是在多長時間內實現,其實并沒有說明。因此銷售凈利率是單一的資金視角下的指標。
2、而內部收益率的含義分解來看,是內部 + 收益率;內部指的是時間范圍,是在成本投出+收益返回全過程中實現,即內部收益率具備了時間的效益。
收益率,在沒有任何的定語前提下,默認為投入了多少,收益了多少?也就是從投入成本的視角看待收益,并且看待在何時獲取收益。
IRR(內部收益率)較銷售凈利率來說,具備了時間效益。
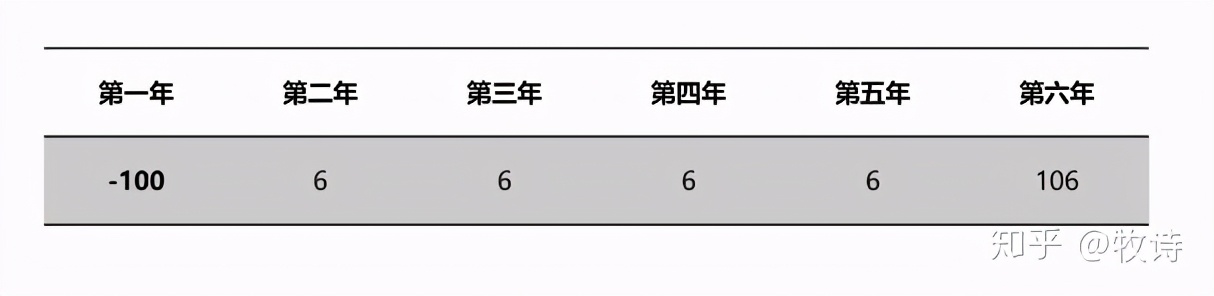
【例2】張三購買了一筆理財產品,模式為先結息后返本。第一年原始投入100萬,第二年開始至第五年收到收益返還,每年6萬,第六年收回本金利息合計106萬,則張三的投資收益是多少呢?
在這個案例中,衡量方法從邏輯上有以下幾種:
方案A:
一種是計算總的利潤為:每年6萬 × 獲利5年 =30萬,本金花了100萬,收益率為:30 / 100×100% =30%,這樣看來這筆理財取得的收益率極高。
方案B:
計算邏輯與A類似,總利潤為:每年6萬 × 獲利5年 =30萬,本金花了100萬,但是取得這筆利潤花了六年的代價,所以收益率應為:30 / 100×100% / 6 =5%
這樣看來,這筆理財每年取得的收益率其實并不高。
方案C:從現金流的角度出發,以時間為單位,衡量不同年度的凈流入流出,得到下表:

IRR公式算出:IRR(-100~106,0.01)=6%
在以上三種不同的邏輯下計算出的收益率完全不一致,原因在于對于收益率的看待視角不同。
方案A:只在乎靜態的取得,不在乎取得這筆利潤所花費的時間代價,即這筆利潤是五年實現還是三年實現完全不同。
而這種計算方法在黃金時代的地產投資是出現過的,因為時間性在市場激進的時候是被選擇性忽視的。
方案B:在A的基礎上考慮了一定的時間性影響,但是是簡單的根據平均性的原則,在一定程度體現了年化收益,但是對于明確的現金流流入流出的測算,利用時間平均線收益原則,并不能完全體現出項目的投資收益。
那么,根據方案C作出的收益率6%代表了什么含義呢?
含義1:體現資金的使用效率。
即如果張三沒有100萬的本金,需要找過橋資金借的話,那么借款利率為6%的時候,用以投資該項目,將一無所獲,正負相抵。
該筆資金的使用效率為6%,找到對于6%借款利率的借款進行投資,可以賺取資金使用效率的差價。
含義2:體現通貨膨脹/貨值貶值率。
即張三名義上的投資報酬率為年化6%,但是由于通貨膨脹是持續發生的,貨值貶值也是持續發生的,因此當通貨膨脹率達到6%的時候,所謂的收益其實是正負抵消了。
含義3:是一種可以衡量未來收益在此刻價值的指標率。
可以從兩個角度來理解:一是從現在看未來,那就是理想的收益率;二是從未來看現在,那就是必須的折現,收益與折現其實是站在不同的時態的產物。
因此IRR既是收益率又是折現率,取決于如何使用。
所以銷售凈利率與IRR的關系應該是:
銷售凈利率為負,IRR無所謂正負了,失去了意義;銷售凈利率為正,IRR通常情況為正,大小取值取決于融資排布/銷售節奏/資金監管等因素。
IRR三兄弟算法:IRR、XIRR與MIRR
1、明確了IRR的含義,那如何計算IRR呢?
在投資測算模型中,常見的函數模型如下:
①當現金流為年度凈現金流時:=IRR(選取的凈現金流,Guess);
②當現金流為季度/月度凈現金流時:=POWER(1+IRR(選取凈現金流,Guess),N)-1,當現金流按季度排布時,N=4;按月度時,N=12;
利用Excel計算IRR,采用的方法是迭代法,迭代的核心邏輯圍繞IRR的官方定義:當凈現值(NPV)=0時的折現率(Rate),NPV是凈現值,也就是說還有原值與現值,兩者之間是在時間的作用下產生的價值變化。
誠如上述分析,從現在的視角看未來的邏輯等同于從過去的視角看現在,因此,收益率的高低應該與折現的高低是一致的。
Excel計算法的內核就是圍繞這個邏輯展開,假設一個可能的Rate,代入看是否吻合,不是繼續逼近,反復計算,直至誤差<0.00001%。
如果運算超過預設迭代次數仍然無法求解,顯示#NUM!.
但是迭代法的需要一個起點,也就是所謂的Guess,其實可能性的IRR的可能落腳點,也就是可能的Rate。
Guess的取值通常在1%~10%之間,也就是IRR的迭代起點從1%開始還是10%開始。
當IRR的取值明顯與凈現金流的表現不相符時,調整Guess也是一種方式。
2、IRR的局限性與兄弟指標(XIRR與MIRR)
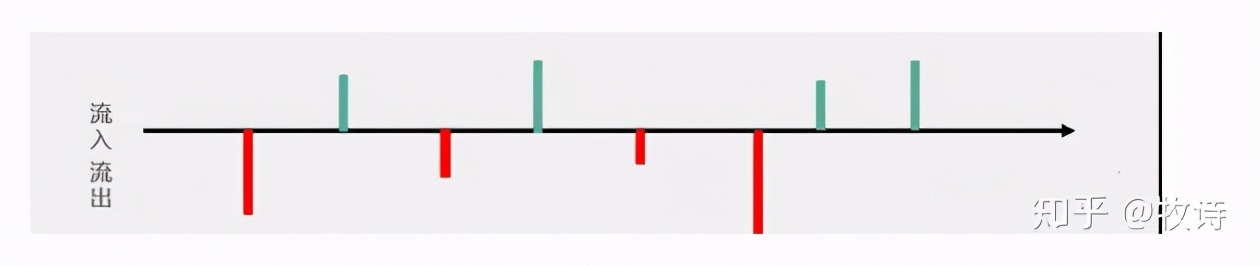
在日常測算過程中,選取進行IRR測算的凈現金流往往并不是理想狀態的IRR。
就像上圖一樣,出現了正向的凈現金流后,還會有大量的資金投入,即凈現金流返負。
正值屬于投資期收回的資金,收回資金如何運用會影響報酬率;負值屬于額外再投入的資金。
在上述例題中:IRR(-100~106,0.01)=6%
按道理分析:
100×(1+6%)^5 應該與100 = 6 / (1+IRR) + 6/(1+IRR)^2 + 6/(1+IRR)^3+ 6/(1+IRR)^4 + 106/(1+IRR)^5相等。
可事實上,兩者之間并不相等,這是為什么呢?
在上述案例中,從第二年起,每年收回的收益,是否再次進行復投是關鍵,每年的收益如果按照IRR的收益率重復投資,則在第六年時,本息和與后者算法一致。
也就是對于出現的重復性的正向現金流是否復投?出現的負向現金流是否再次融資,成為影響IRR準確性的關鍵因素。
傳統的IRR是無法體現這一變化的,因此,IRR的孿生兄弟MIRR,俗稱改良IRR很好地彌補了IRR本身的局限。
MIRR的核心邏輯為:期間所有的收回的資金(現金流入),全部以再投資率計算終值;期間所有的投入的資金(現金流出),全部以融資利率計算現值。
見下圖:
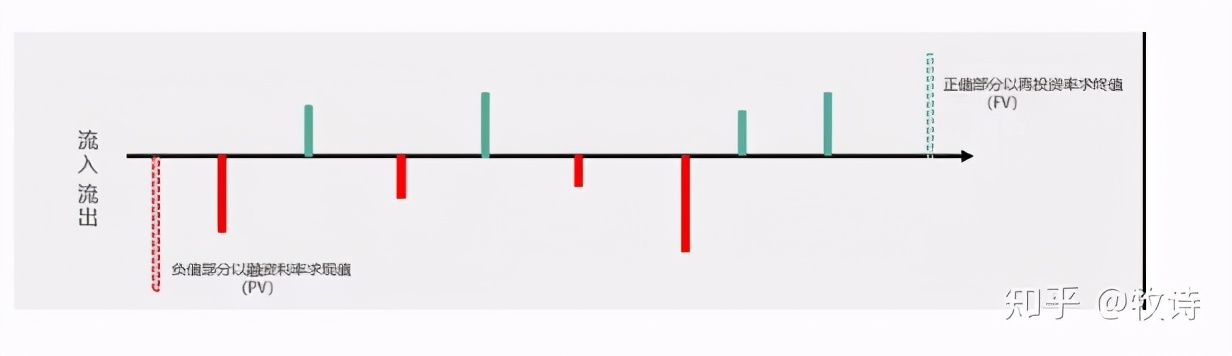
因此,MIRR在IRR的公式基礎上,多了兩項指標:MIRR(選取凈現金流,融資利率,再投資利率)
對重復返負的凈現金流考慮其融資利率,對于過程中回正的凈現金流考慮去再投資收益,是MIRR的核心思想。
如果說MIRR是在現金流準確性上對IRR進行一定程度的改良和彌補,那IRR的另一個兄弟XIRR則很好的彌補了IRR在時間效益上的局限:
為什么這么說呢?
在日常計算IRR的范圍內,似乎并沒有額外強調這個IRR必須是時間間隔相等的凈現金流對應的。
從其函數公式也可以看出,IRR的公式并沒有填寫時間的位置。
而XIRR是使用時凈現金流必須為月度現金流,且間隔相等。
但現金流不一定定期發生即且需要將每月的凈現金流按照統一的標準定位時間,如:2020年9月,XIRR會默認這個凈現金流的取值是這個月的某一特定天對應的數字。
因此較IRR計算的準確性較高一些。
因此,XIRR在IRR的公式基礎上,多了一項指標:XIRR(選取凈現金流,對應日期,Guess)
追求靜態的利潤已經是過時的需求了,追求現金流的重復使用與現金流貢獻本身賺取的時間周期效益帶來的利潤難道不香嗎?